Предыстория.
У меня есть хороший друг. Тоже «радиолюбитель», самоучка и весьма энергичный молодой человек. Так вот. Попался ему как-то в руки сгоревший «синим пламенем» источник бесперебойного питания (ИБП) – не лучший образец продукции «поднебесной». Починить его оказалось неподъемной задачей. Однако, трансформатор оказался одним из «живучих» элементов, и Дима задумал изготовить небольшой преобразователь 12В в 220В для какого-то применения (в купе с автомобильным аккумулятором) на дачном участке. Немного погуглив и собрав кучу распечаток из Интернета, он обратился ко мне (зная мои поделки на Ардуино) со странным вопросом: «А «красивую» синусоиду твоя Ардуина может генерить?»

А вот тут и начинается текст по делу 🙂

Итак. Синусоида. Значит из цифр (которыми оперирует Ардуинка) нам нужно получить аналоговый сигнал… А значит нам нужен Цифро-Аналоговый Преобразователь (или ЦАП, или DAC -по ненашему).
Меня это не сильно испугало. Я уже сталкивался с ЦАП-ми, а конкретнее в детстве паял вариант R-2R. Те, кто постарше наверняка помнят такие чудесные поделки, как Covox ( http://ru.wikipedia.org/wiki/Covox ). В те годы (примерно 90-ые), мне только доводилось мечтать о звуковой карте, а вот вышеупомянутое устройство, да еще сделанное своими руками – доставило столько приятных минут 🙂
Итак, сказано – сделано!
Ну, будучи до конца честным, признаюсь. Я для начала поискал готовые решения для Ардуино в просторах Интернета. (Вот один из вариантов, с применением ШИМ-сигнала: http://electronics.stackexchange.com/questions/41738/possible-to-output-sinusoidal-signal-with-an-arduino. Не понравился.)

Итак, нам нужено изготовить простейший цифро-аналоговый преобразователь: R-2R.
Вот буржуйское описание: http://en.wikipedia.org/wiki/Resistor_ladder

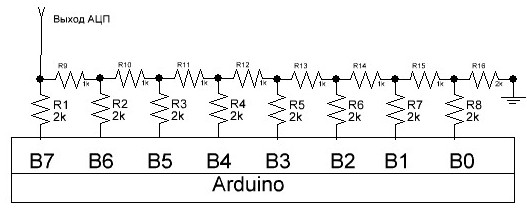
(B7..B0 — это биты, B7 — старший, B0 — младший).
Своё название (R-2R) данный ЦАП получил из-за номиналов применяемых в нём резисторов с сопротивлениями R и 2*R. Сопротивления по идее могут быть любыми (1k-2k; 10k-20k и т.д). Однако, я чаще всего встречал варианты с номиналами 1k и 2k.
Как же эта штука работает?
Каждый вход ЦАПа вносит свою лепту в выходной сигнал пропорционально своей «значимости». Т.е. левый вход оказывает самое большое влияние на выходной сигнал (половина опорного напряжения), следующий за ним ¼ , следующий – 1/8 и т.д. Ну а самый последний (правый) вход изменяет выходной сигнал на ничтожные милливольты. Подставляя значение битов на входе ЦАП выходное напряжение можно рассчитать так:
Uвых=Uпит * (B7 * 1/2 + B6 * 1/4 + B5 *1/8+ B4*1/16+B3*1/32+B2*1/64+B1*1/128+B0*1/256).
Если выставить на вход ЦАП-а значение 255 (бинарное 11111111), то получаем самый высокий выходной сигнал. Если же 00000000 — ноль.
Uпит – напряжение питания микроконтроллера. Таким образом, наш восьмибитный ЦАП способен выдать 256 различных напряжений с шагом около 20 милливольт, при опорном напряжении 5 Вольт.
Желательно чтобы ЦАП (8-ми разрядный, как у нас) был подключен к целому порту. Тогда выводить любое значение в ЦАП — будет очень просто:

PORTD = 215;

Итак, прикидываем на макетке:

Проверяем работоспособность, засылая в порт различные значения. Мультиметром замеряем напряжение на выходе — все очень хорошо. Можем двигаться дальше. С «железной» частью вроде как разобрались.

Теперь математическая составляющая.
Вооружившись школьным учебником алгебры (шучу… шучу, конечно же Википедия!) вспоминаем, что такое Синусоида: http://ru.wikipedia.org/wiki/Синусоида

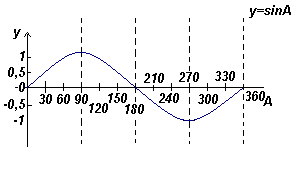
Адаптируем к нашим условиям. ЦАП может выдавать значения от 0 до 255. Причем, за нулевое значение (мы будем оперировать только целыми положительными числами) примем 127. Длительность волны примем 255 шажков (опять же для удобства). Т.е., для одного периода значение функции поменяется 255 раз. Естественно, чем больше «шажков» мы уместим в этот период, тем точнее получим синусоиду.

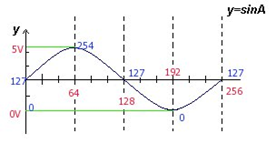
Синим цветом я постарался обозначить значения напряжения, получаемые на выходе ЦАП, при «контрольных» значениях точек на оси Х.
Общая формула синусоиды:
Y=a+b*SIN(c*X)

Итак, наша синусоида стартует со значением 127 (для ЦАП) и заканчивается этим значением. Для этого, вводим значение смещения по оси У а=127. a характеризует сдвиг графика по оси Oy. Чем больше a, тем выше поднимается график.

Значение синуса может меняться от -1 до 1 (Кто бы мог подумать!!!). Чтобы растянуть график по вертикали, вводим второе значение b, характеризующее растяжение графика по оси Oy. Чем больше увеличивается b, тем сильнее возрастает амплитуда колебаний; Ну, тут тоже понятно, что при максимальном значении в (254-127) b=127

с характеризует растяжение графика по оси Ox.

Длина периода =2*Pi. Мы условились, что этот период мы делим на 255 «шагов». Т.е., 255-ый шаг должен иметь значение 2*Pi. Для нашего случая С=2*Pi*(1/255) или 2*Pi*0.0392 или Pi*0.007843
Окончательно получаем следующую формулу расчета: Y=127+127*SIN(Pi*X*0.007843).
(Желающие получить БОЛЕЕ точные результаты, могут использовать, допустим 512 шажков. Только нужно пересчитать константу).

Давайте проверим нашу формулу на «ключевых» значениях X:
0 (0) = 127
64 (Pi/2) =253
128(Pi) =125
192 (3*Pi/2) =0
255 (2Pi) =126

Весьма правдоподобно. Итак далее, тут можно поступить двумя способами: высчитывать значение по ходу дела – способ НАВЕРНЯКА не самый быстрый, а можно заранее рассчитать эти значения и брать их из таблицы. Я предпочел второй способ.
Программист из меня не важный (Бейсик – в детстве, Паскаль – в школе, ФОРТРАН – в институте), поэтому я не стал тратить время на поиски того же Борланд паскаля или изучение Питона, «напрягом» знакомого программиста… Как впрочем и на калькуляторе высчитывать 255 значений мне показалось «времярасточительным» занятием. НО у меня же есть Ардуинка! (И я ОЧЕНЬ стараюсь использовать ее по полной программе.). Вот ее и заставим произвести нужные мне расчеты.

/*
Расчет таблицы для значений синусоиды, с выводов в монитор ком-порта
*/
void setup(){
  Serial.begin(9600);
}

void loop(){
for (int i=0;i<256;i++) {
  Serial.print(byte(127+(127*sin(PI*i*0.007843))));
  Serial.print(", ");
}
delay(10000); // Задержка, чтобы успеть скопировать :)
}

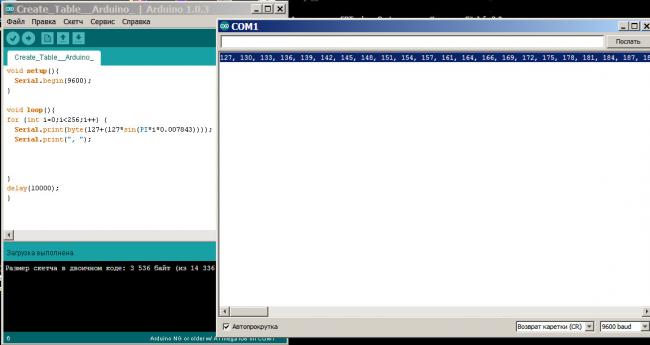
Вот наша таблица значений :

127, 130, 133, 136, 139, 142, 145, 148, 151, 154, 157, 161, 164, 166, 169, 172, 175, 178, 181, 184, 187, 189, 192, 195, 197, 200, 202, 205, 207, 210, 212, 214, 217, 219, 221, 223, 225, 227, 229, 231, 232, 234, 236, 237, 239, 240, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 251, 252, 252, 253, 253, 253, 253, 253, 253, 253, 253, 253, 253, 252, 252, 251, 251, 250, 249, 249, 248, 247, 246, 245, 243, 242, 241, 239, 238, 236, 235, 233, 231, 230, 228, 226, 224, 222, 220, 218, 215, 213, 211, 209, 206, 204, 201, 199, 196, 193, 191, 188, 185, 182, 180, 177, 174, 171, 168, 165, 162, 159, 156, 153, 150, 147, 144, 141, 137, 134, 131, 128, 125, 122, 119, 116, 112, 109, 106, 103, 100, 97, 94, 91, 88, 85, 82, 79, 76, 73, 71, 68, 65, 62, 60, 57, 54, 52, 49, 47, 44, 42, 40, 38, 35, 33, 31, 29, 27, 25, 23, 22, 20, 18, 17, 15, 14, 12, 11, 10, 8, 7, 6, 5, 4, 4, 3, 2, 2, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 16, 17, 19, 21, 22, 24, 26, 28, 30, 32, 34, 36, 39, 41, 43, 46, 48, 51, 53, 56, 58, 61, 64, 66, 69, 72, 75, 78, 81, 84, 86, 89, 92, 96, 99, 102, 105, 108, 111, 114, 117, 120, 123, 126,

Набрасываем скетчик для вывода значений таблицы в ЦАП:

/*
Ghost D. 2013
DAC R/2R
Это генератор синусоиды с частотой 50Гц
*/

unsigned char sin_tab [256] = {
127,130,133,136,139,142,145,148,151,154,157,160,164,166,169,172,175,178,181,184,187,189,192,195,197,200,202,205,207,210,212,214,217,219,221,223,225,227,229,231,232,234,236,237,239,240,242,243,244,245,246,247,248,249, 250,251,251,252,252,253,253,253,253,253,254,253,253,253,253,252,252,251,251,250,249,249,248,247,246,245,243,242,241,239,238,236,235,233,231,230, 228,226,224,222,220,218,215,213,211,209,206,204,201,199,196,193,191,188,185,182,180,177,174,171,168,165,162,159,156,153,150,147,144,141,137,134,131,128,125,122,119,116,112,109,106,103,100,97,94,91,88,85,82,79,76, 73,71,68,65,62,60,57,54,52,49,47,44,42,40,38,35,33,31,29,27,25,23,22,20,18,17,15,14,12,11,10,8,7,6,5,4,4,3,2,2,1,1,0,0,0,0,0,0,0,0,0,0,1,1,2,2,3,4,5,6,7,8,9,10,11,13,14,16,17,19,21,22,24,26,28,30,32,34,36,39,41,43,46,48,51,53,56,58,61,64,66,69,72,75,78,81,84,87,89,93,96,99,102,105,108,111,114,117,120,123,127};

void setup() { DDRD =0xFF;}

void loop() {
for (int i=0;i<256;i++) {
  PORTD=sin_tab[i];
  delayMicroseconds(75);
}
}

Вроде как и все. Но, как говорят французы, "аппетит приходит во время еды", а именно, оказывается нужно две синусоиды...
А, была-не была. Тем более, столько уже проделано. Макетим.

"Допиливаем" скетч, сделаем небольшое смещение синусоид offset 128. (Кстати, огромная благодарность Юре, за идею "склейки" пинов для получения "полного" порта).

/*
DAC R/2R 50Hz
Ghost D. 2013
Это генератор синусоид с частотой 50Гц
*/

unsigned char sin_tab [256] = {
127,130,133,136,139,142,145,148,151,154,157,160,164,166,169,172,175,178,181,184,187,189,192,195, 197,200,202,205,
207,210,212,214,217,219,221,223,225,227,229,231,232,234,236,237,239,240,242,243, 244,245,246,247,248,249, 250,251,
251,252,252,253,253,253,253,253,254,253,253,253,253,252,252,251, 251,250,249,249,248,247,246,245,243,242,241,239,
238,236,235,233,231,230, 228,226,224,222,220,218, 215,213,211,209,206,204,201,199,196,193,191,188,185,182,180,177,
174,171,168,165,162,159,156,153, 150,147,144,141,137,134,131,128,125,122,119,116,112,109,106,103,100,97,94,91,88,
85,82,79,76, 73,71,68,65,62,60,57,54,52,49,47,44,42,40,38,35,33,31,29,27,25,23,22,20,18,17,15,14, 12,11,10,8,7,6,5,
4,4,3,2,2,1,1,0,0,0,0,0,0,0,0,0,0,1,1,2,2,3,4,5,6,7,8,9,10,11,13,14,16,17,19,21,22,24, 26,28,30,32,34,36,39,41,43,46,
48,51,53,56,58,61,64,66,69,72,75,78,81,84,87,89,93,96, 99,102,105,108,111,114,117,120,123,127};

void setup()
{
  DDRD = 0xFF;
  DDRC |= 0b00111111; // PC0-PC5
  DDRB |= 0b00011000; // PB3-PB4
}

void pp(unsigned char i)
{
  // (PORTC & 0b11000000) - Обнуляем только используемые биты
  // i >> 2 - сдвигаем (отбрасываем первые 2 бита, которые будем выводить в порт Б
  // (PORTC & 0b11000000) | (i >> 2) выставляем только оставшиеся 5 бит в порту С
  PORTC = (PORTC & 0b11000000) | (i >> 2);
  // (PORTB & 0b11100111) - обнуляем только три используемых бита
  // (i & 0b00000011) - обнуляем неиспользуемые биты
  // (PORTB & 0b11100111) | (i & 0b00000011) - выставляем нужные биты в порту Б
  PORTB = (PORTB & 0b11100111) | (i & 0b00000011);
}

#define offset 128

void loop() {
for (int i = 0, j = i + offset; i < 256; i++, j++) {
  PORTD = sin_tab[i];
  pp(sin_tab[j]);
  if (j == 255) j = 0;
  delayMicroseconds(75);
}
}

Делаем контрольный замер, подключив выходы ЦАП-ов к осциллографу (красиво совмещаем выдаваемые Ардуинкой синусоиды):

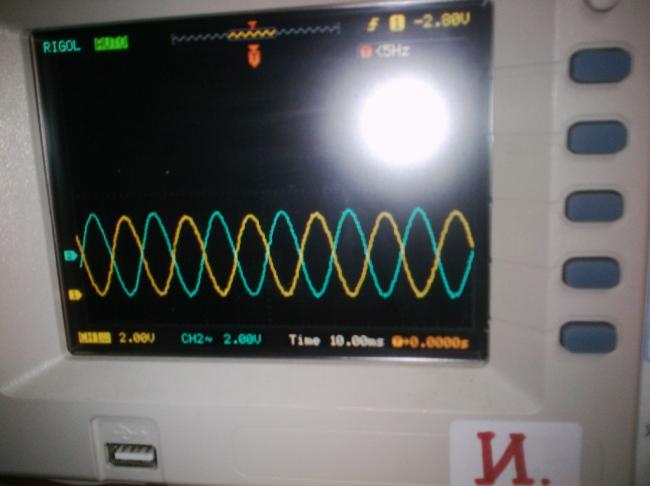
Красота! То, что и желали получить. Все, мой приятель остался очень доволен. Я отдал ему прошитую Atmeg-у для дальнейшего применения.

Про дальнейшую судьбу его устройства - это отдельная история, не входящая в рамки данного опуса.
P.S. Вот фото того устройства, ради которого все это и было проделано 🙂