Введение в робототехнику
перевод лекций профессора Стенфордского университета Осамы Кхатиба (Oussama Khatib), 2008 год
Лекция 2
Пространственное описание, обобщенная система координат, переходные системы координат (от базы к клешне), матрица поворота, пример матрицы поворота, преобразование из одной системы координат в другую, образец гомогенного преобразования, операторы преобразования.
Здравствуйте!
Сегодня мы с вами начнем рассматривать базовые преобразования необходимые для кинематических расчетов. Как я упомянул на прошлой лекции — описание взаимосвязи локальных систем отсчета (имеется ввиду системы привязанные к звеньям, далее проясниться) и преобразований между ними является важным аспектом. Мы начинаем с преобразований которые позволят нам рассчитывать положение «клешни» относительно базы робота (базовой системы координат).
Очевидно, что когда мы определяем расположение следующего звена, нам нужно уметь преобразовывать из исходной системы координат, иными словами описывать позицию и ориентацию звена относительно текущего звена. Нам с вами потребуется обсудить каким образом представлять координаты объекта и его ориентацию в пространстве, выбрать из существующих способов.
Так же я собираюсь описать в некоторой мере объект управления, манипулятор, и что представляют его звенья, что такое степени свободы манипулятора, как мы можем представлять себе позицию манипулятора в пространстве. Итак манипулятор представляет из себя набор звеньев (также links — связей), связанных между собой кинематических пар. Начальное звено зафиксировано – оно называется базой. А последнее звено именуется клешней (gripper – хвататель, кому знакомо точное название поправьте меня). Главная задача, суть манипулятора – это управление и перемещение этой клешни, которая, в свою очередь, выполняет прикладные задачи.
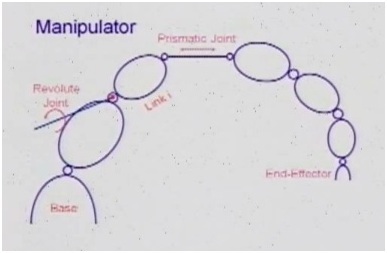
base – база, end-effector – клешня, link – звено, revolute joint – шарнирное соединение (петлевое в дальнейшем), prismatic joint – телескопическое соединение (скользящее).
Как мы понимаем, основной интерес представляет перемещение конечного звена и одновременно положение остальных звеньев в пространстве. Как видно на рисунке выше, сущесвует два варианта возможных соединений – вращательное и поступательное (скольжение).
Они производятся относительно одной оси,если рассматривать его по формуле Чебышева – Граблера – Кутцбаха, имеют одну степень свободы. Как я уже сказал у нас есть звенья и совакупность этих звеньев назовем буквой n. Мы будем понимать под n число движущихся звеньев + 1 закрепленное звено (базу). В начале мы будем рассматривать в момент времени только одну степень свободы, одну кинематическую пару, соединять ее с предыдущей (следующей) и так далее.
Если мы имеем шарнирное соединение сколько степеней свободы оно имеет?
-Три (одно в случае «плоского» соединения), поскольку для описания ориентации в пространстве нам нужна связка из трех параметров.
Допустим нам нужно описать звено, для того чтобы точно описать его в пространстве, достаточно трех точек, на рисунке они указаны векторами.

Благодаря этому мы определили расположение звена, но каждый вектор в свою очередь имеет три параметра (координаты конечной точки), таки образом мы получаем 9ть параметров для определения только одного звена, умножим это на n, может получиться приличное количество!
Большое число параметров. И это является неотъемлемой частью описания. Мы заинтересованы в максимальном сокращении числа этих параметров.
В случае описания звена тремя векторами, на самом деле не требуется 9 параметров, поскольку эти точки связаны с твердым телом и они неподвижны друг относительно друга. А поскольку три точки неподвижны относительно друг друга, то мы можем обойтись и меньшим числом параметров. Вот мы и подходим к обобщенным координатам.
Мы сможем посчитать эти параметры, число совпадет с количеством степеней свободы робота.
Давайте проанализируем количество параметров (именно независимых параметров), которое потребуется чтобы описать конфигурацию манипулятора в пространстве обобщенных координат.
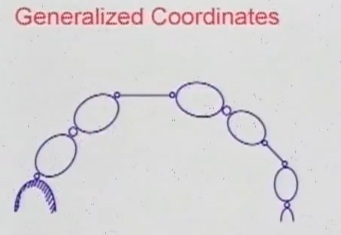
Итак у нас есть манипулятор и для того чтобы сосчитать, какое число степеней свободы, удалим соединения
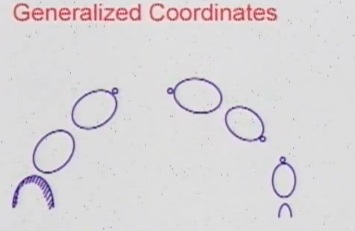
Таким образом мы имеем n звеньев (твердых тел) в пространстве. Если мы возьмем одно из них,то для того чтобы описать его в пространстве нам требуется 6 параметров – три для позиции в пространстве и три для ориентации. Для всех звеньев нам понадобиться 6n параметров. Теперь вернемся к ограничениям – связям между звеньями. Соединение сокращает число параметров каждого звена на 5ть (за исключением шарнирного соединения). Тем самым мы имеем целых 5n ограничений.
В случае петлевого соединения (при рассмотрении звена принимаем возможности только его перемещения с учетом варианта соединения) звено не имеет возможности перемещаться в пространстве, также оно не может вращаться в пространстве, остается только возможность вращения в плоскости, перпендикулярной к оси проходящей через петлевое соединение.
В случае скользящего соединения мы имеем возможность поступательного перемещения только вдоль одной оси, нет возможности ни вращаться, ни перемещаться в двух оставшихся осях.
Итак вернемся к количеству звеньев n. По отдельности они имеют 6n степеней свободы, но каждое соединение привносит 5ть ограничений (оставляет звену только одну степень свободы), а соединений у нас тоже n, если совершить нехитрое действие и вычесть из 6n-5n мы придем к выводу что число степеней свободы равно количеству звеньев механизма (d.o.f –степень свободы degrees of freedom).
Это правило распостраняется только на роботов с фиксированным начальным звеном, в случае гуманоидного робота это правило недействительно.
Если рассмотреть клешню робота, то в описание ее положения можно включить множество параметров остальных звеньев зависящих между собой и это неправильно, для описания нужно использовать только независимые параметры, эти параметры формируют оперативное пространство.

Как мы уже выяснили избыточным будет описание положения клешни при помощи трех векторов, в этом случае m=9. А как насчет Эйлера? Эйлер предложил описывать трехмерные пространства с помощью кватернионов. (не стоит закрывать страницу — до таких глубин курс опускаться не будет, пока, Осама нормальный мужик, разжует как следует).
В случае представления по Эйлеру будут свои проблемы связанные с непрерывностью вращения, но об этом после.
Вы что-нибудь слышали о матрицах поворота? О направляющих косинусах?
Мы поговорим и об этом. Итак у вас есть две системы координат с одним началом и разной ориентацией, вам нужно найти взаимосвязь между ними. И если вы возьмете матрицу 3х3, она позволит вам описать одну систему относительно другой.
Итак эта матрица включает набор направляющих косинусов. Она дает описание ориентации одной системы относительно другой, а если к этому добавить еще и вектор указывающий на положение в пространстве, то у нас выйдет 12 параметров. Мы рассмотрим в дальнейшем случаи когда нам придется пойти таким путем в расчетах.

А сейчас рассмотрим оперативные координаты – координаты рабочей точки. Если мы смотрим на точку действия, то, на что робот воздействует, наши оперативные координаты совпадут с точкой воздействия, если использовать приспособления, сварочный модуль, то рабочая точка переместиться дальше, в то место, где будет происходить взаимодействие.
Рабочая точка определяется 6ю независимыми параметрами, число независимых параметров необходимых для описания мы назовем m0(set of independent parameters), напоминаю, что общее число (зависимых) параметров имеет индекс m.
Если рассматривать робот-манипулятор на плоскости, то для описания движения клешни нам понадобиться 2 параметра для позиции клешни и 1 для направления. Всего 3. Рассмотрим робота с тремя вращательными соединениями (тетта1, тетта2, тетта3) работающего в плоскости.
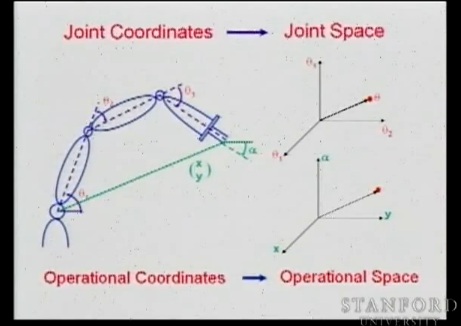
Поведение этого робота целиком задается этими тремя координатами.
Представим этот манипулятор как точку в 3D пространстве. с координатными осями тетта1, тетта2, тетта3. Это называется пространством конфигурирования (увы это мой термин, прямого перевода я не нашел, так что если кто знает пишите профперевод “joint space”). В пространство конфигурирования мы также можем разместить препятствия возникающие на пути робота.
Вернемся к позиционированию клешни, ее координаты для нашего «плоского» робота задаются при помощи x и y, но помимо этого нам еще нужен один угол альфа для того чтобы его сориентировать на плоскости.
Теперь когда мы знаем параметры описания позиции клешни мы можем описать оперативные координаты (также в 3D).
Итак мы имеем теперь оперативное пространство и пространство конфигурирования (надеюсь вам как и мне что-то начинает проясняться), а теперь добавьте к роботу еще одно звено. Получается, что оперативное пространство не поменялось, а вот пространство конфигурирования стало четырехмерным и у нас появилась избыточность, то есть не влияя на рабочую точку звенья могут занимать разные положения.
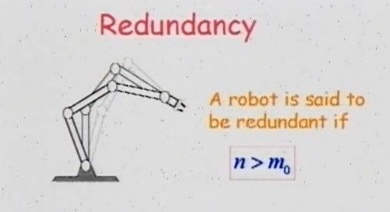
Мы пришли к заключению, что робот имеет избыточность в том случае, когда число звеньев n (число степеней свободы механизма) превышает число независимых параметров m0 (параметров оперативного пространства).
Возможность различного подхода к конечной точке является преимуществом, с помощью этого у нас появляется возможность обходить препятствия и добираться до труднодоступных мест, как например внутренности кабины авто на сборочном конвейере. Но сейчас мы остановимся на роботах без альтернативных положений.
Мы рассмотрим простые модели которые приведут нас к прямому методу кинематического расчета.
Давайте спросим себя, что описывает точку в пространстве относительно какой-то базы, базовой точки? Кончено это вектор. Мы с вами начнем заниматься описанием положения точки относительно системы координат. Нам предстоит научиться выводить описание и взаимосвязь векторов описанных в разных системах координат.
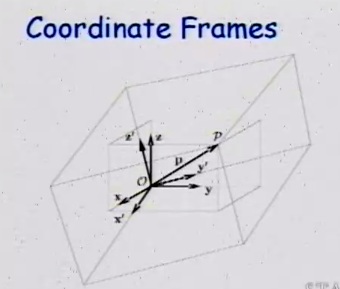
напимер нам потребуется научиться выводить описание вектора в системе координат имеющей поворот относительно базовой системы, также смещение:
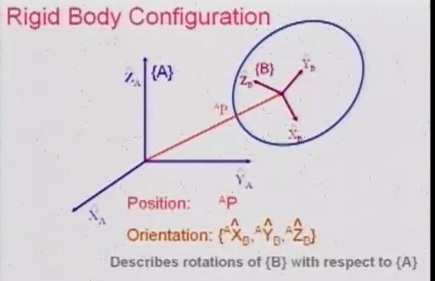
Мы имеем твердое тело описываемое системой {B}, однако относительно системы {A}, твердое тело описывается благодаря вектору Pa (символ a повествует о том что вектор описан в системе {A}), а также ориентации в пространстве.
Остановимся на ориентации в пространстве. Если откинуть смещение, вектор Pa, то нам остается разобраться с поворотом, для этого используется матрица поворота.

Здесь обратите внимание на вывод, выходит что матрица поворота состоит из приведенных в другую систему ортов какой-либо системы координат

Например надпись во второй строке третьем столбце гласит, что мы должны подставить туда значение проекции орта оси Z системы B на орт оси Y системы A, с учетом знака!
(Если не разобрались:
Описание ориентации — это в первую очередь описание положения системы, а именно ее ортов относительно каждого орта базовой системы, выраженного в градусах.
Орт — единичный вектор, проложенный на оси координат от нуля до единицы.
Обратите внимание на строки в этой матрице — в первой, множителем является орт Х системы А, то есть мы описываем углы между ортами системы В и ортом Х системы А(Х — если первая строка) при помощи косинуса этого угла, далее на второй строке мы уже описываем углы между ортами системы В и ортом Y тоже шпарим косинусы между ними, ну и так далее
!Внимание! То, что написано в этих скобках нужно понять и запомнить — это пройдет сквозь весь курс и на основе этого мы еще многое будем делать.)
Ну и примерчик для затравки
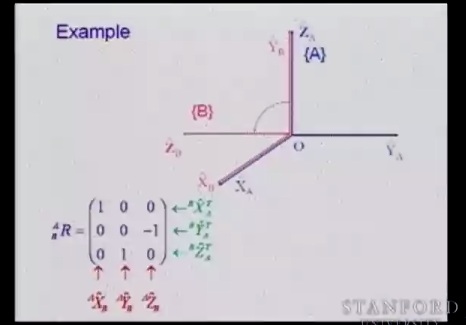
Первый столбец:
1 – потому что оси x совпадают, нули потому, что орт x в других осях равен нулю (проекция — это точка), ну и так далее.

Обратите внимание, что матрица поворота одной системы (A) относительно другой (B) равна транспонированной матрице поворота системы B относительно A.
Итак, теперь когда мы уже представляем себе матрицу поворота, опишем необходимые преобразования для представления положения одной системы относительно другой
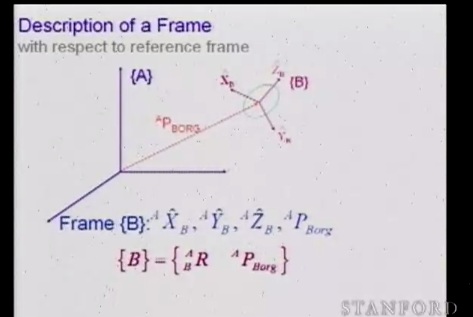
Как видим, описание разделено на две части: определение вектора смещения Paborg (вектор смещения описанный в пространстве координат A) и матрицы поворота.
Опираясь на наши знания давайте опишем положение вектора Pb в системе А, для этого нам и пригодится матрица поворота.
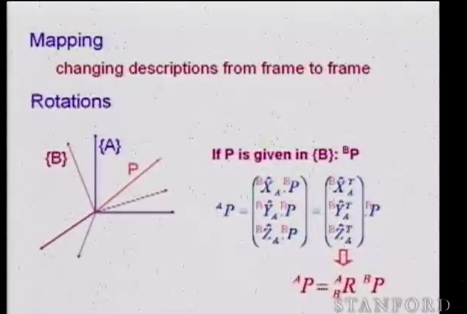
А теперь давайте рассмотрим смещенную систему относительно другой без изменения ориентации в пространстве.
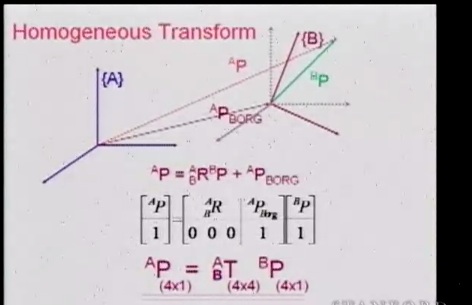
Итак, точка расположена в пространстве B и описана вектором P. Та же точка описывается в пространстве другой системы уже другим вектором – Pa, который попросту равен сумме вектора смещения и вектора положения точки в системе B. Просто, однако эта простота позволительна только для данного частного случая.
Рассмотрим общую форму преобразования. Пусть мы имеем точку в пространстве B, сама же система координат B смещена и повернута относительно системы A.
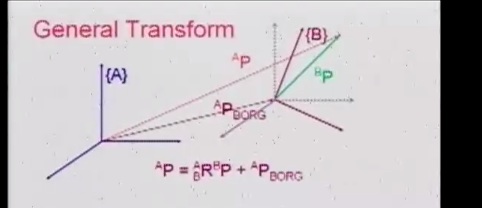
Тогда, в отличие от рассмотренного до этого случая, нам необходимо не просто сложение, а сложение членов описанных в одной системе координат, т.е сложение Pborg и вектора Pb, описанного в системе A. Для этого нам потребуется умножить вектор Pb на матрицу поворота.
Ну вот мы и описали общую форму преобразования. Теперь применяя это к звеньям мы могли бы двигаться от одного звена к другому и так далее. Но это не совсем так, это не просто матрица поворота, где зная первую матрицу поворота между A и B, чтобы перевести A из B в C потребуется умножить еще на одну матрицу.
В этом случае нам нужно обращать внимания на суммы. И самое лучшее что можно сделать для упрощения переходов из системы в систему это перевести все в гомогенную форму. Но как это сделать в случае сложения двух пространственных векторов в трехмерном пространстве? Нам нужно перейти в четырехмерное пространство, тогда нам удастся перейти в гомогенную форму и упростить преобразования. И как это сделать?
-Добавить еще одну строку.
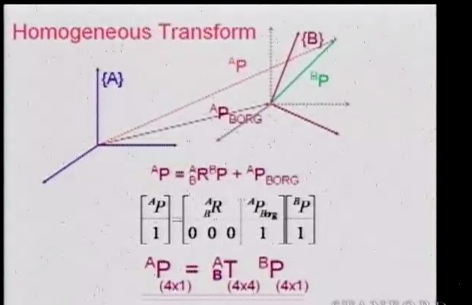
Теперь для перехода из одной системы в другую нам нужно будет всего лишь домножать на еще одну матрицу. Вот в чем заключается преимущество гомогенного преобразования.
А теперь рассмотрим пример основанный на предыдущем
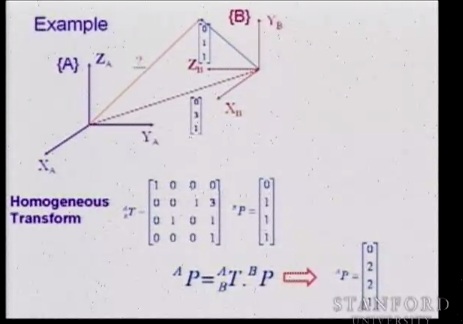
Если вспомнить предыдущий пример, то мы имели систему повернутую относительно другой на 90 градусов против часовой стрелки вдоль оси X. Матрица поворота прежняя, составляет часть матрицы T (элемент второй строки, третьего столбца =-1, просто тут не разглядеть), к ней добавляется вектор смещения(напомню, что представление вектора в виде матрицы, например вектора смещения, это просто 0 по оси x (так и есть ведь мы сдвигаемся в плоскости YZ) , далее 3 – это три орта по оси Y и 1 – один орт по оси Z).
Вот в чем преимущество гомогенного преобразования.
После всего сказанного стоит отметить еще однин нюанс. Матрица поворота также может использоваться для преобразования векторов в одной системе

Вот пример
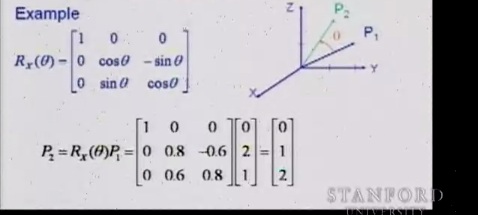
Матрицы поворотов относительно осей можно взять на википедии.
Все это применимо для переноса положения точки из одной системы координат в другую, только теперь мы не будем задумываться о том как описать эту точку в обоих системах мы просто перенесем ее при помощи оператора Q.

(Не знаю зачем он об этом вроде уже все разжевал, видимо хотел показать что смещение это вектор Q.)
Теперь рассмотрим инверсное преобразование. В рамках инвертирования матрица поворота из A в B просто транспонируется. А перенос представляется как описание расстояния в системе B.
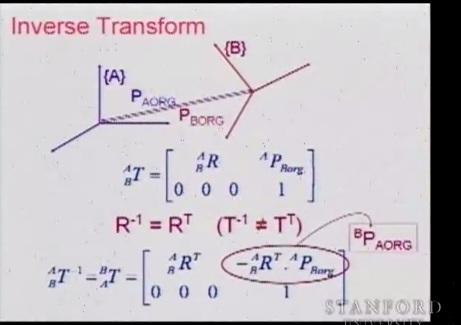
Итак теперь мы знаем прямое преобразования и инверсное, это поможет нам описывать кинематику в последующих лекциях.
До следующей лекции!

0 комментариев на «“Введение в робототехнику (перевод лекций курса introduction to robotics). Лекция 2”»
Все хорошо, но в данном примере в отличии от первого (вводная часть) без перевода стенографии лекции не обойтись, т.е. без основ термеха и ТДиМ тут мало чего понятно, для новичка и первого входа каша маслянная. А вот бегло пробежал по стенографии и пояснения к рисункам обрели смысл, может поправите? А так в общем и целом с опорной базой знаний — отлично воспринимается.
Ждем продолжения.
Вот ссылочка на стенографию, вот этот бы перевод в литературной обработке дал бы больше знаний, это конечно ИМХО.
Ну видите ли, я и переводил по стенографии, частично с нее по крайней мере. Дело в том, что стенографию надо адаптировать — ведь там устная речь, много оговорок. Тем более скорость человеческой речи позволяет ему так или иначе вдалбливать смысл в слушателя (процент пустых фраз велик и суть из них надо вылавливать).
Но я надеюсь, что с последующими лекциями целостная картинка появиться. Желаю не терять интереса!
Кстати я хочу сказать, что тут полезно прочитать хотя бы два раза и кое что выписать, тогда материал усвоиться. Ну а что касается доп. знаний, то на данном этапе это капелька теормеха — звенья только, да степени свободы. Я вам скажу, что я тоже валенок в этом, ну я думаю если интерес есть — освоить можно.
Лекции очень понятные, я этот материал долго искал. Если по книгам сравнивать, то там в самом деле требуется еще 2 книги минимум — входной барьер. А здесь он объясняет, если что не ясно. Там кстати на видео люди на его вопросы не очень то резво отвечают вот он и возвращается к основам частенько.
Вот тут я и вспоминаю своего препода термеха, где мы все были бандерлогами и урюпинцами, а потом корреляцию решали на раз и два, в стенографии смысла много скрыто, но возможно даёт свой перевес имеющаяся база, но для новичка сложно, ваш труд оценен высоко, спасибо и респект, но он не для новичка, новичек уснет на второй картинке, нет экшена, а на лекциях автора студенты в экшене, смысл я думаю ясен…
Если честно, то очень сложно для входа, очень…
Я Вас не сужу, не думайте, просто на ресурсе нужен материал доступный для вхождения. Людям пришедшим в первой сложно нас понять. А в стенографии идет прямой диалог, и там много пинальной информации в направленном векторе на изучение, т.е. он дает пинок где и что копать и в какую сторону ползти, ну или лететь после пинка… )))