Искусственные нейронные сети (ИНС – она же нейросеть (neuronet)) – звучит таинственно и загадочно. Пахнет искусственной жизнью и могуществом ИИ.

Между тем, эти математические структуры давно прочно вошли в наш быт:
автоматизация процессов распознавания образов,
адаптивное управление,
прогнозирование,
и т.д..

Основу нейронной сети составляет нейрон — элемент, который имитирует работу нейронов мозга.

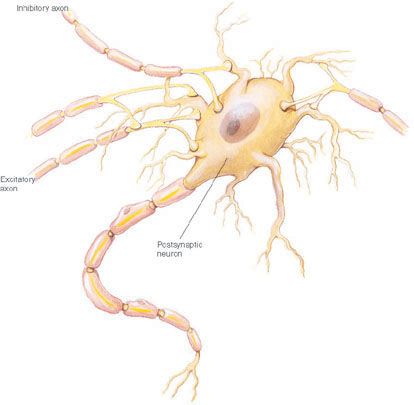
Нейрон характеризуется своим состоянием и, по аналогии с реальным нейроном, может быть либо возбуждён — либо заторможен.

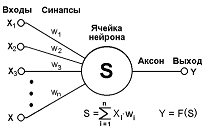
Как видно – у нейрона есть входы (синапсы), которые соединены с выходами других нейронов. И есть выход (аксон) сигнал с которого поступает на синапсы других нейронов.
Каждый синапс характеризуется величиной синаптической связи – её так же называют весом Wi.

По физическому смыслу, вес синоптической связи – это электрическая проводимость данного синапса.

Состояние нейрона определяется, как сумма состояний его входов.

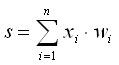
Как видим – значение на входе синапса умножается на вес данного синапса, потом все эти значения суммируются и получаем текущее состояние нейрона.

	float sum = 0;
	for(int i = 0; i < N; i++) {
		sum += inputs[i]*weights[i];
	}

Значение на выходе нейрона – это функция от его состояния.

Y = f(s)

Функция f называется активационной и может иметь различный вид:

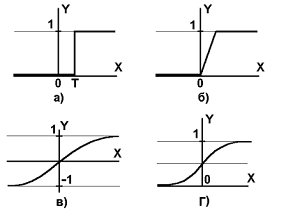
Чаще всего, используется логистическая функция или функция S-образного вида(сигмоид):

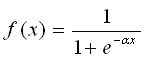
#define  NN_FUNC_SIGMA_LOGISTIC(x) ( 1 / (1 + exp(-(x))) )
...
value = NN_FUNC_SIGMA_LOGISTIC( sum );

Одна из причин, по которой сигмоид используется в нейронных сетях, это простое выражение его производной через саму функцию (которое и позволило существенно сократить вычислительную сложность метода обратного распространения ошибки, сделав его применимым на практике):

S'(x) = S(x)*(1 - S(x))

решение:

           1
S(x) = -----------
       1 + exp(-x)

            exp(-x)        1 + exp(-x) - 1      1             1
S'(x) = --------------- = ---------------- = ----------- - ---------------
        (1 + exp(-x))^2    (1 + exp(-x))^2   1 + exp(-x)   (1 + exp(-x))^2

теперь, если вынести S(x) за скобки, то и получим требуемое выражение.

Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.

Формально, искусственный нейрон – является однослойным перцептроном (персептроном), т.е. моделью, в которой входные элементы напрямую соединены с выходными с помощью системы весов, и выполняет функцию линейной классификации.

Классификация – это процесс группировки/разбиения объектов исследования или наблюдения в соответствии с их общими признаками.

Линейный классификатор - это один из самых простых алгоритмов классификации.
В задачах с двумя классами (бинарная классификация) линейный классификатор - это гиперплоскость, разделяющая n-мерное пространство признаков на два класса (полупространства).
Т.е. нейрон (линейный классификатор) определяет - входные данные относятся либо к группе A, либо к группе B.
Это можно представить, если рассмотреть линию в 2-мерном пространстве.
Точки в этом пространстве могут быть классифицированы, как лежащие либо по одну сторону этой линии, либо по другую.

Однослойный перцептрон хорош для решения задач линейной классификации, т.е. именно для случая двумерного пространства и классифицирующей линии, но он не сможет решить задачу, которая не может быть решена линейным разделением.
Классический пример задачи, которая не по зубам однослойному перцептрону - исключающее ИЛИ (XOR - exclusive OR).

Рассмотрим точки (0,0), (1,0), (0,1), и (1,1) в пространстве.
Для XOR, не существует способа провести одну линию, которая отделяет точки TRUE: (1,0) и (0,1) от точек FALSE: (0,0) и (1,1).

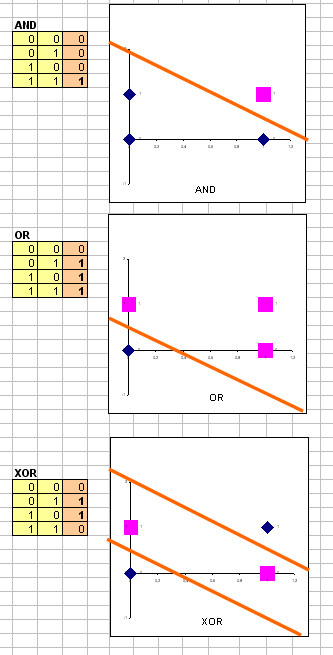
Т.о. точки XOR линейно неразделимы.
Выходит, однослойный перцептрон не может быть обучен, для разделения по XOR.

Чтобы решить проблему XOR, нужно создать многослойный перцептрон!
Для решения задачи XOR, многослойный перцептрон будет иметь два входа, затем "скрытый" слой, и один выход.

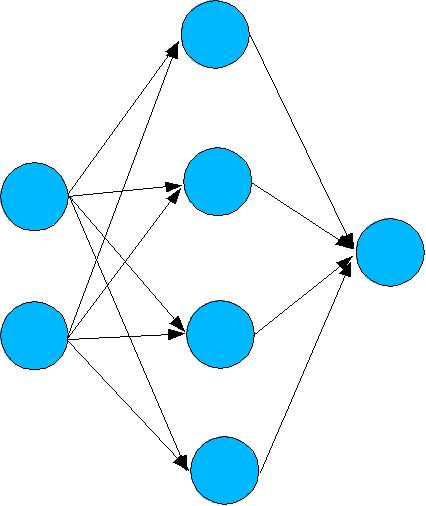
Скрытый слой - это, фактически, несколько нейронов, которые сообща справляются с одной и той же задачей.

Т.о. если взять группу нейронов, объединить их в слои, то мы получим эту таинственную Искусственную Нейронную Сеть!

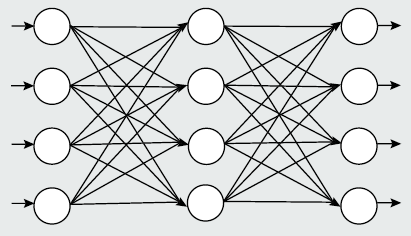
- самый распространённый тип ИНС - многослойный перцептрон.
Как видим, данная сеть состоит из трёх слоёв (обычно их называют – входной (сенсорный), скрытый и выходной). Нейроны каждого слоя соединены по принципу «каждый с каждым».

Теоретически, число слоев и число нейронов в каждом слое, может быть произвольным. Однако, в реальности, оно ограничено ресурсами компьютера или микросхемы, на которых реализуется данная ИНС 😉
Выбор структуры ИНС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации.

Выбор структуры ИНС определяется решаемой задачей:
Пример 1:
простая нейронная сеть для решения задачи логического И/ИЛИ/искл. ИЛИ
Два нейрона первого(входного) слоя, 4 нейрона скрытого слоя и один нейрон на выходе.
Пример 2:
нам нужно распознать, символ цифры на матрице 10x10, то входной слой будет состоять из 100 нейронов – по нейрону на ячейку. А выходной слой должен иметь столько нейронов, сколько символов для распознавания. Т.к. нужно распознавать цифру – то должно быть 10 выходных нейронов. Со скрытым слоем такой определённости нет 🙂
Пример 3:
ещё пример, который сразу приходит на ум – это входные нейроны на каждый рецептор робота, а выходные нейроны на каждый исполнительный механизм 🙂

Итак, у нас есть ИНС, однако, очевидно, что её функционирование зависит от величин синаптических связей. Поэтому, необходимо подобрать оптимальные величины этих переменных для решения поставленной задачи. Этот этап и называется обучением ИНС.

Как видим, в попытке создания ИИ методом копирования природы мы приходим к тем же терминам, что используются в нашей жизни 🙂

Обучение ИНС может вестись с учителем или без него.

При обучении с учителем – ИНС задаются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей.

Сразу вспоминается школа и зубрёжка таблицы умножения 🙂

При обучении без учителя - выходы ИНС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.

Вот мы и познакомились с ИНС.
Всего несколько минут чтения, а от таинственности ИНС не осталось и следа 😉 Даже как-то грустно, что это ,всего лишь, матрицы коэффициентов 🙁
«Формула жизни» опять ускользнула в туман загадок 🙂

Однако, это ничуть не умаляет возможностей ИНС и скоро мы с ними познакомимся 🙂

далее: Принцип обучения многослойной нейронной сети с помощью алгоритма обратного распространения

Ссылки
http://ru.wikipedia.org/wiki/Искусственный_нейрон
http://ru.wikipedia.org/wiki/Сигмоид
http://en.wikipedia.org/wiki/Perceptron
http://ru.wikipedia.org/wiki/Перцептрон
http://www.machinelearning.ru/
http://www.basegroup.ru/library/analysis/neural/math/
http://www.intuit.ru/department/ds/neuronnets/
Материалы по нейронным сетям
Нейросеть в 11 строчек на Python
Derivative of the Sigmoid function

По теме
Пример работы самоорганизующейся инкрементной нейронной сети SOINN