В данной статью я расскажу вам о том как повысить точность периодов выполнения участков кода программы. Для реализации материала статьи вам потребуется совершенно любая плата Arduino и больше ничего.
Перед рассмотрением материала позволю себе небольшое лирическое отступление. С платформой Arduino, я пока что знаком, можно сказать, по наслышке, но для Windows программирую много и давно, так же имею техническое образование по радиоэлектронике, по сему особых преград для освоения данной области не вижу. Первым своим роботехническим проектом решил сделать восьминогого робота паука, для создания которого мной были приобретены сервоприводы НК151138 фирмы HobbyKing и специализированная плата формфактора-Arduino, на базе контроллера ATMega1280, с возможностью удобного подключения большоего числа сервоприводов. Вот эта плата.
Но о своих успехах в создании робота я расскажу в следующих своих статьях, так как в настоящий момент неоценимыми усилиями Почты России порог моего дома преодолела только заявленная выше плата arduino, сервоприводы в настоящий момент бороздят безграничные просторы Китайской Почты, по этой причине моя первая статья будет реализована исключительно с применением возможности платы.
Не редко при создании конструкций нам необходимо выполнять какие-либо участки кода с определенной периодичностью, например 1 раз в одну секунду, чаще всего для этой цели применяют задержку delay, которая для случая с периодом 1 секунда должна равняться 1000, так как значения задаются в миллисекундах, на первый взгляд все должно работать точно и без особых проблем, так как значения задержек в контроллерах ATMega отрабатывается с высокой точностью, так как стандартное значение тактовой частоты для большинства контроллеров равно 16 Мегагерцам (1,6+E7), то значение задержки 1 миллисекунда вычисляется как одна 160000 от тактовой частоты. Тактовая частота контроллера определяется резонансной частотой кварцевого генератора, которая обладает достаточно высокой точностью и обычно измеряется в миллионных долях от номинальной частоты, обозначаемых как ppm (part per m illion) или 1•10 -6. Для большинства современных, дешевых кварцевых резонаторов точность составляет около +-30ppm, так же в пределах рабочего температурного диапазона возможно отклонение от рабочей частоты на +-50ppm, так же при эксплуатации изделия в течении 1 года возможен дрейф в количества +-5ppm. Таким образом присовокупив все возможные факторы можно аппроксимировать все погрешности в один показатель, который можно назвать как максимальное ожидаемое отклонение и его можно принять для простоты за +-100ppm. Таким образом при данном отклонении значение частоты кварцевого генератора может принимать значения 16000000+-1600Гц (15998400-16001600), поделив эти отклонения на значение частоты имеем слудующие апсолютные значения:(0,9999 — 1,0001). Теперь рассчитаем пределы возможных отклонений на реальных временных периода, например 1 час, 1 сутки, 1 месяц, 1 год
Максимальное отклонение за:
1 час — 0,36 секунд
1 сутки — 8,64 секунды
1 месяц (30 дней) — 259,2 (4 минуты 19,2 секунды)
1 год (365,25 дней) — 3155,76 секунд (52 минуты 35,76 секунд)

Как вы могли заметить, точность достаточно неплохая, тем более, что вы редко столкнетесь с подобной погрешностью, ведь вам придется найти самый неудачный экземпляр в партии имеющий при номинальное температуре отклонение +-30ppm, при этом этот экземпляр должен будет проработать 4 года при максимально(или минимально) возможной темпиратуре, да и вообще вам должно очень сильно «неповезти» (: В реальный условиях кварцевые резонаторы дают не более 3-5минут отклонения за 1 год. Теперь давайте же преступим к рассмотрению первого, на первый взгляд очевидного примера применения функции delay для организаций заданной задержки выполнения операции.

unsigned long Event = 0;//Счетчик количества событий
int TimeOut = 1000;//Таймаут повторения события

void setup()
{
  Serial.begin(9600);
  //Инициализация последовательного порта
}

void loop()
{
  Serial.print("Number of events: ");
  Serial.print(Event);
  Serial.print("\t Time from start: ");
  Serial.println(millis());
  //Вывод результата в консоль
  Event++;//Итеррация счетчика
  delay(TimeOut);//Таймаут
}

Загружаем скетч, жмем Ctrl+Shift+M и наблюдаем в консоли следующий вывод: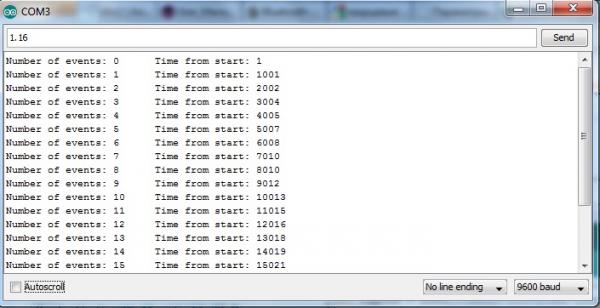

По всей видимости что-то не так:) Уже на первых секунда выполнения мы видим что операция выполняется не раз в 1000 миллисекунд. Теперь дадим данному процессу немного времени и имеем следующий вид:

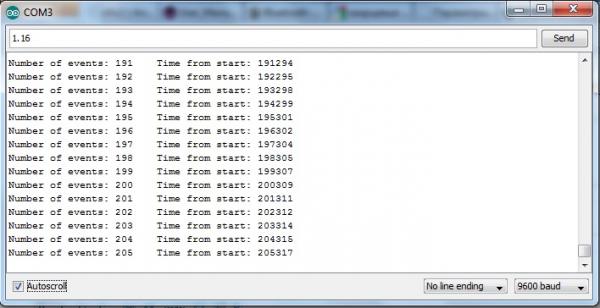
Как видите величина ошибки стала еще более существенной, и так будет продолжаться и далее. С чем это связано? Дело в том, что выполнение кода так же требует определенного времени, и задержка delay выполняется после того как это время затрачено, следовательно из второго рисунка можно сказать, что на выполнение кода 200 раз у контроллера ушло 309 миллисекунд времени, а кода почти нет, следовательно в реальных программах, где код будет более существенным, например будут присутствовать циклы с большим числом итераций или работа с массивами или числами с плавающей запятой, значение накапливающийся ошибки будет значительно выше. Как бороться с подобной неточностью? Выход очень простой необходимо уменьшать значение задержки delay на величину того времени, которое было затрачено на выполнение кода, как это сделать смотрим код ниже:

unsigned long Event = 0;//Счетчик количества событий
int TimeOut = 1000;//Таймаут повторения события

void setup()
{
  Serial.begin(9600);
  //Инициализация последовательного порта
}

void loop()
{
  Serial.print("Number of events: ");
  Serial.print(Event);
  Serial.print("\t Time from start: ");
  Serial.println(millis());
  //Вывод результата в консоль
  Event++;//Итеррация счетчика
  delay(TimeOut - millis()%TimeOut);//Таймаут
}

Как видите достаточно добавить в вызов delay столь простые изменения и точность повысится в разы. Смотрим как выглядит консоль:

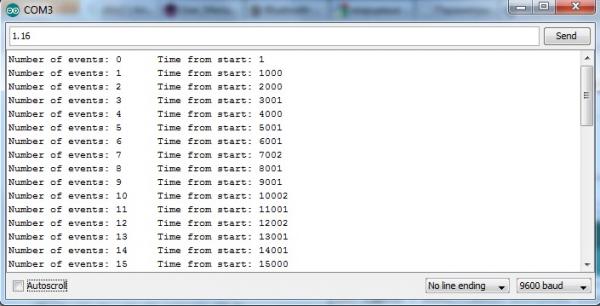
На первый взгляд может показаться, что ошибка все равно имеется, но если дать этому процессу сколько угодно времени настоятся вы увидите что значение этой ошибки всегда будет в этих небольших пределах, смотрим следующий скрин:

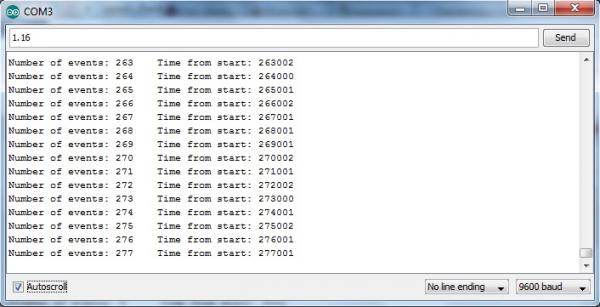
Как видите ошибка осталось той же и на больших периодах ей можно пренебречь. Стоит отметить, что данный метод будет работать если значение таймаута меньше чем время выполнения контроллером кода, хотя это и так очевидно:)

Далее попробую немного развить данную статью в направлении дальнейшего повышения точности. Если кому-то не хватает «кварцевой» точности вашей ардуино системы, вы можете повысить её за счет следующих действий.
1)Необходимо либо вычислить реальное отклонение точности за большой период (например использую интернет сервисы точного времени) либо измерив прецизионным частотомером частоту вашего кварцевого генератора при номинальных условиях.
2)Необходимо вычислить, раз в какой период «набегает» ошибка в одну миллисекунду.
3)Сделать в исходнике счетчик выполненных циклов от прошлой корректировки времени и осуществлять его итерацию при каждом цикле. Далее необходимо завести константу хранящую количество циклов за которое «набегает» 1 миллисекунда. Завести переменную для корректировки, которая будет равна по умолчанию 0. При каждом цикле проверять равенства счетчика циклов с момента прошлой корректировки и константы и в случае равентсва, необходимо обнулить счетчик и присвоить переменной для корректировки значение 1, если ваш кварц отстает, либо -1 если он спешит. Добавить корректировочную переменную в вызов delay. После вызова delay добавить условие — если счетчик циклов с момента корректировки равен 0 обнулить переменную корректировки. Исходник будет иметь примерно такой вид:

unsigned long Event = 0;//Счетчик количества событий
int TimeOut = 1000;//Таймаут повторения события
unsigned long Correct = 0;//Счетчик количества событий c
//с момента прошлой корректировки
unsigned long isCorrect = 5;//константа определяющая
//индивидуальную погрешность конкретного кварцевого
//резонатора и означающая, что раз в это количество циклов
//необходимо прибавить (или отнять если значение отрицательное)
 //1 миллисекунду к функции delay для приведения системы
 //к истенному показателю точности времени
int Delta = 0;//Переменная для корректировки
void setup()
{
  Serial.begin(9600);
  //Инициализация последовательного порта
}

void loop()
{
  Serial.print("Number of events: ");
  Serial.print(Event);
  Serial.print("\t Time from start: ");
  Serial.println(millis());
  //Вывод результата в консоль
  Event++;//Итеррация счетчика
  Correct++;
  if (Correct == isCorrect)
  {
    Correct = 0;//Обнуление счетчика
    Delta = 1;//Корректировка
  }
  delay(TimeOut - millis()%TimeOut+Delta);//Таймаут
  if (Correct == 0) Delta = 0;
}

Всем удачи!