26. OpenCV шаг за шагом. Обработка изображения - операторы Собеля и Лапласа

На прошлом шаге, мы рассмотрели операцию свёртки и отметили, что свёртка — это очень полезная и распространённая операция, лежащая в основе различных фильтров.

Одна из важнейших свёрток – это вычисление производных.

В математике и физике производные играют очень важную роль, то же самое можно сказать и про компьютерное зрение 🙂
Но что же это за производная от изображения? Всё очень просто! Как мы помним, изображения, с которыми мы работаем, состоят из пикселей, которые, для картинки в градациях серого, задают значение яркости.
Т.е. наша картинка — это просто двумерная матрица чисел. Теперь вспомним, что же такое производная.

Производная (функции в точке) — это скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

Получается, что, в нашем случае, производная — это отношение значения приращения пикселя по y к значению приращению пикселя по x:

dI = dy/dx;

Работая с изображением I, мы работает с функцией двух переменных I(x,y), т.е. со скалярным полем. Поэтому, более правильно говорить не о производной, а о градиенте изображения.

Градиент (от лат. gradiens — шагающий, растущий) — вектор, показывающий направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля).

Если каждой точке M области многомерного пространства поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле.

Итак, градиент для каждой точки изображения (функция яркости) — двумерный вектор, компонентами которого являются производные яркости изображения по горизонтали и вертикали.

grad I(x,y) = (dI/dx, dI/dy);

В каждой точке изображения градиентный вектор ориентирован в направлении наибольшего увеличения яркости, а его длина соответствует величине изменения яркости.

вектор (в заданной точке) задаётся двумя значениями: длиной и направлением.
длина:

sqrt( dx^2 + dy^2 );

направление — угол между вектором и осью x:

atan(dy/dx);

Для дифференцирования изображения используется, так называемый, оператор Собеля.

Оператор Собеля — это дискретный дифференциальный оператор, вычисляющий приближение градиента яркости изображения.
Оператор вычисляет градиент яркости изображения в каждой точке. Так находится направление наибольшего увеличения яркости и величина её изменения в этом направлении. Результат показывает, насколько «резко» или «плавно» меняется яркость изображения в каждой точке, а значит, вероятность нахождения точки на грани, а также ориентацию границы.

Т.о. результатом работы оператора Собеля в точке области постоянной яркости будет нулевой вектор, а в точке, лежащей на границе областей различной яркости — вектор, пересекающий границу в направлении увеличения яркости.

Наиболее часто оператор Собеля применяется в алгоритмах выделения границ.

Оператор Собеля основан на свёртке изображения небольшими целочисленными фильтрами в вертикальном и горизонтальном направлениях, поэтому его относительно легко вычислять. Оператор использует ядра 3×3, с которыми свёртывают исходное изображение для вычисления приближенных значений производных по горизонтали и по вертикали.

Уффф.. сколько всего понаписано, сколько страшных математических слов, а использовать этот оператор в OpenCV легко и просто!

В OpenCV оператор Собеля реализуется функцией cvSobel()

CVAPI(void) cvSobel( const CvArr* src, CvArr* dst,
                    int xorder, int yorder,
                    int aperture_size CV_DEFAULT(3));

— вычисление производной изображения (градиента), используя оператор Собеля (aperture_size = 1,3,5,7) или Щарра (aperture_size = -1)

src — исходное изображение
dst — изображение для сохранения результа
xorder — порядок производной по x (0,1 или 2)
yorder — порядок производной по y (одновременно нулевой может быть только либо xorder, либо yorder)
aperture_size — размер ядра оператора Собеля (1,3,5,7)

-1 0 1
-2 0 2
-1 0 1

— для x (для y — получается транспонированием)

при aperture_size==-1 используется оператор Щарра (Scharr)

-3  0 3
-10 0 10
-3  0 3

— для x (для y — получается транспонированием)

#define CV_SCHARR -1
#define CV_MAX_SOBEL_KSIZE 7

UPD 2014-11-30
в новой версии библиотеки OpenCV для оператора Щарра завели отдельный метод:
Scharr()
см.
Sobel()
Sobel Derivatives

чтобы избежать переполнения целевое изображение должно быть 16-битным (IPL_DEPTH_16S) при 8-битном исходном изображении.
Для преобразования получившегося изображения в 8-битное можно использовать cvConvertScale() или ConvertScaleAbs()

CVAPI(void)  cvConvertScale( const CvArr* src, CvArr* dst,
                             double scale CV_DEFAULT(1),
                             double shift CV_DEFAULT(0) );
#define cvCvtScale cvConvertScale
#define cvScale  cvConvertScale
#define cvConvert( src, dst )  cvConvertScale( (src), (dst), 1, 0 )

— изменение типа массива (с опциональным изменением масштаба)
— линейная трансформация каждого элемента исходного массива (у многоканального изображения каждый канал обрабатывается отдельно)
формула:

   dst(x,y,c) = scale*src(x,y,c)+shift

(функцию можно использовать для изменения типа изображения)

src — исходное изображение
dst — изображение для сохранения результа
scale — масштаб
shift — сдвиг — величина добавляемая к каждому элементу

CVAPI(void)  cvConvertScaleAbs( const CvArr* src, CvArr* dst,
                                double scale CV_DEFAULT(1),
                                double shift CV_DEFAULT(0) );
#define cvCvtScaleAbs  cvConvertScaleAbs

-выполняет линейное масштабное преобразование изображения
dst(x,y,c) = abs(scale*src(x,y,c)+shift).

! данная функция работает только с изображениями типа 8u (8-битные беззнаковые) — в других случаях может быть использовано: cvConvertScale() + cvAbsDiffS() !

Пример, демонстрирующий работу оператора Собеля:

//
// пример работы оператора Собеля - cvSobel()
//
// robocraft.ru
//

#include <cv.h>
#include <highgui.h>
#include <stdlib.h>
#include <stdio.h>

IplImage* image = 0;
IplImage* dst = 0;
IplImage* dst2 = 0;

int xorder = 1;
int xorder_max = 2;

int yorder = 1;
int yorder_max = 2;

//
// функция-обработчик ползунка - 
// порядок производной по X
void myTrackbarXorder(int pos) {
	xorder = pos;
}

//
// функция-обработчик ползунка - 
// порядок производной по Y
void myTrackbarYorder(int pos) {
	yorder = pos;
}

int main(int argc, char* argv[])
{
	// имя картинки задаётся первым параметром
	char* filename = argc >= 2 ? argv[1] : "Image0.jpg";
	// получаем картинку
	image = cvLoadImage(filename, 1);
	// создаём картинки
	dst = cvCreateImage( cvSize(image->width, image->height), IPL_DEPTH_16S, image->nChannels);
	dst2 = cvCreateImage( cvSize(image->width, image->height), image->depth, image->nChannels);

	printf("[i] image: %s\n", filename);
	assert( image != 0 );

	// окно для отображения картинки
	cvNamedWindow("original", CV_WINDOW_AUTOSIZE);
	cvNamedWindow("sobel", CV_WINDOW_AUTOSIZE);


	int aperture = argc == 3 ? atoi(argv[2]) : 3;

	cvCreateTrackbar("xorder", "original", &xorder, xorder_max, myTrackbarXorder);
	cvCreateTrackbar("yorder", "original", &yorder, yorder_max, myTrackbarYorder);

	while(1){

		// проверяем, чтобы порядок производных по X и Y был отличен от 0
		if(xorder==0 && yorder==0){
			printf("[i] Error: bad params for cvSobel() !\n");
			cvZero(dst2);
		}
		else{
			// применяем оператор Собеля
			cvSobel(image, dst, xorder, yorder, aperture);
			// преобразуем изображение к 8-битному
			cvConvertScale(dst, dst2);
		}

		// показываем картинку
		cvShowImage("original", image);
		cvShowImage("sobel", dst2);

		char c = cvWaitKey(33);
		if (c == 27) { // если нажата ESC - выходим
			break;
		}
	}

	// освобождаем ресурсы
	cvReleaseImage(& image);
	cvReleaseImage(&dst);
	cvReleaseImage(&dst2);
	// удаляем окна
	cvDestroyAllWindows();
	return 0;
}

скачать иcходник (26-cvSobel.cpp)

первая производная по x — весёлый я:

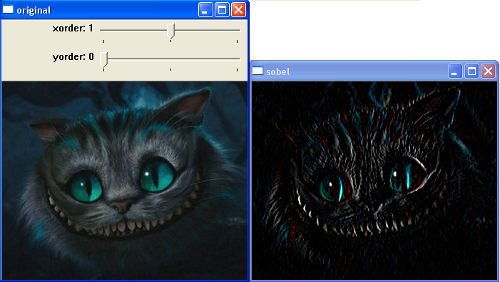
первая производная по y — демонический я:

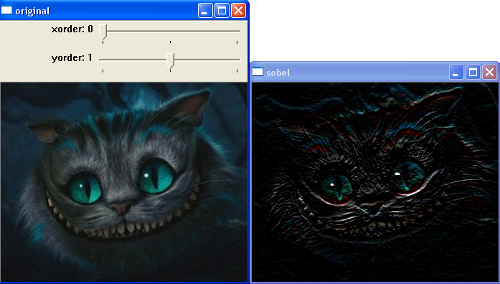
Оператор Собеля представляет собой неточное приближение градиента изображения, но он достаточно хорош для практического применения во многих задачах.
Однако, с увеличением градиентного угла, у оператора Собеля, с ядром 3×3, растут неточности, которые, однако, можно компенсировать используя оператор Щарра (просто представляет другую версию ядра 3х3).

Так же, как вы уже поняли, оператор Собеля — это свёртка изображения с ядром с заданными коэффициентами. Так что можете просто использовать эти коэффициенты в примере из прошлого шага и посмотреть, что из этого выйдет 😉

Раз уж мы рассмотрели оператор Собеля, можно заодно отметить и оператор Лапласа, который позволяет вычислить т.н. лапласиан изображения — суммирование производных второго порядка.
OpenCV содержит для этого функцию cvLaplace():

CVAPI(void) cvLaplace( const CvArr* src, CvArr* dst,
                      int aperture_size CV_DEFAULT(3) );

— получает лапласиан изображения (d2/dx + d2/dy)I
фактически, это оператор собеля с xorder = yorder = 2

исходное изображение может быть формата 8u или 32f
результирующее изображение может быть формата 16s или 32f

//
// пример работы оператора Лапласа - cvLaplace()
//
// robocraft.ru
//

#include <cv.h>
#include <highgui.h>
#include <stdlib.h>
#include <stdio.h>

IplImage* image = 0;
IplImage* dst = 0;
IplImage* dst2 = 0;

int main(int argc, char* argv[])
{
	// имя картинки задаётся первым параметром
	char* filename = argc >= 2 ? argv[1] : "Image0.jpg";
	// получаем картинку
	image = cvLoadImage(filename, 1);
	// создаём картинки
	dst = cvCreateImage( cvGetSize(image), IPL_DEPTH_16S, image->nChannels);
	dst2 = cvCreateImage( cvGetSize(image), image->depth, image->nChannels);

	printf("[i] image: %s\n", filename);
	assert( image != 0 );

	// окно для отображения картинки
	cvNamedWindow("original", CV_WINDOW_AUTOSIZE);
	cvNamedWindow("cvLaplace", CV_WINDOW_AUTOSIZE);

	int aperture = argc == 3 ? atoi(argv[2]) : 3;

	// применяем оператор Лапласа
	cvLaplace(image, dst, aperture);

	// преобразуем изображение к 8-битному
	cvConvertScale(dst, dst2);

	// показываем картинку
	cvShowImage("original", image);
	cvShowImage("cvLaplace", dst2);

	cvWaitKey(0);

	// освобождаем ресурсы
	cvReleaseImage(& image);
	cvReleaseImage(&dst);
	cvReleaseImage(&dst2);
	// удаляем окна
	cvDestroyAllWindows();
	return 0;
}

скачать иcходник (26-cvLaplace.cpp)

а тут я получился, прямо скажем, как-то жутковато 🙂

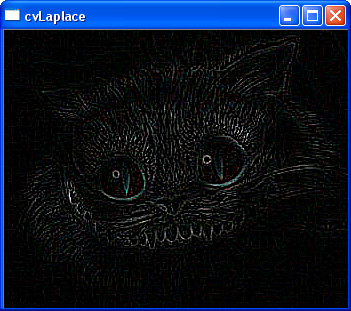
Далее: 27. Обработка изображения — детектор границ Кенни (Canny)

Ссылки
http://ru.wikipedia.org/wiki/Производная_функции
http://ru.wikipedia.org/wiki/Вектор_(математика)
http://ru.wikipedia.org/wiki/Grad
http://ru.wikipedia.org/wiki/Скалярное_поле
http://ru.wikipedia.org/wiki/Оператор_Собеля
http://en.wikipedia.org/wiki/Sobel_operator
http://ru.wikipedia.org/wiki/Лапласиан

0 комментариев на «“26. OpenCV шаг за шагом. Обработка изображения — операторы Собеля и Лапласа”»

JohnJ:

2015-08-09 в 07:24

Не смог использовать в OpenCVSharp метод Scharr, так как он доступен только из Cv2, где требуется не IplImage, а InputArray и OutputArray. Как преобразовать одно в другое — я не смог найти. Нашёл только, что можно сразу изображение считать через Cv2.ImRead(filename), а потом его показывать в окне через window.ShowImage(img.ToCvMat()). Но это совершенно другая история… 🙂 Хотелось бы научиться преобразовывать IplImage и InputArray друг в друга. Знает кто-нибудь как это делается?

Войдите, чтобы ответить

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Преимуществ нет, за исключением читабельности: тип bool обычно имеет размер 1 байт, как и uint8_t. Думаю, компилятор в обоих случаях…

Добрый день! Я недавно начал изучать программирование под STM32 и ваши уроки просто бесценны! Хотел узнать зачем использовать переменную типа…

если у вас черное окно попробуйте так. #include <opencv2/opencv.hpp> #include<iostream> #include <stdlib.h> #include <stdio.h> using namespace cv; using namespace std;…

Для Python 3.4: pip3 install tensorflow-1.1.0-cp34-cp34m-linux_armv7l.whl https://github.com/samjabrahams/tensorflow-on-raspberry-pi

PORTB = (PORTB & 0b11100111) | (i & 0b00000011); А почему Вы обнуляете биты 3 и 4, а заполняете биты…